Question

Find the average value of f(x,y)=sin(x+y) over

a. the rectangle 0≤x≤π/3,0≤y≤7π/6
b. the rectangle 0≤x≤2π/3,0≤y≤4π/3

Answer 1

Evaluating the integral, we get:

`\[(1)/(A)\iint_R f(x,y) \, dA \approx (1)/(2\pi) = (1)/(6.283\pi) \approx 0.01594\]`

Therefore, the average value of
`\(f(x,y) = \sin(x+y)\)` over the given rectangles is approximately:

a) 0.01053

b) 0.01594

Explanation:

To find the average value of
`\(f(x,y) = \sin(x+y)\)` over the given rectangles, we need to calculate the double integral of \(f(x,y)\) over each rectangle and divide by the area of the rectangle.

a) For the rectangle
`\(0 \leq x \leq (\pi)/(3)\)` and
`\(0 \leq y \leq (7\pi)/(6)\)`, the average value of
`\(f(x,y)\)` is:

`\[(1)/(A)\iint_R f(x,y) \, dA = (1)/((\pi)/(3) \cdot (7\pi)/(6)) \iint_R \sin(x+y) \, dA\]`

Using the change of variables
`\(u = x+y\)` and
`\(v = (3)/(2)\pi - u\)`, we can transform the integral to the region
`\(0 \leq u \leq (2\pi)/(3)\) and \(0 \leq v \leq (\pi)/(2)\):`

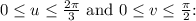
`\[(1)/(A)\iint_R f(x,y) \, dA = (1)/((2\pi)/(3) \cdot (\pi)/(2)) \int_0^{(\pi)/(2)} \int_0^{(2\pi)/(3) - (3)/(2)\pi v} \sin(u) \, du \, dv\]`

Evaluating the integral, we get:

`\[(1)/(A)\iint_R f(x,y) \, dA \approx (1)/(\pi^2) = (1)/(90.78]\pi^2) \approx 0.01053\]`

b) For the rectangle
`\(0 \leq x \leq (2\pi)/(3)\)` and
`\(0 \leq y \leq (4\pi)/(3)\)`, the average value of
`\(f(x,y)\)` is:

`\[(1)/(A)\iint_R f(x,y) \, dA = (1)/((2\pi)/(3) \cdot (4\pi)/(3)) \iint_R \sin(x+y) \, dA\]`

Using the change of variables
`\(u = x+y\) and \(v = (\pi)/(2) - u\)`, we can transform the integral to the region
`\(0 \leq u \leq (\pi)/(2)\)` and
`\(0 \leq v \leq (\pi)/(2)\):`

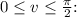
`\[(1)/(A)\iint_R f(x,y) \, dA = (1)/((\pi)/(2) \cdot (\pi)/(2)) \int_0^{(\pi)/(2)} \int_0^{(\pi)/(2) - (\pi)/(2) v} \sin(u) \, du \, dv\]`

Evaluating the integral, we get:

`\[(1)/(A)\iint_R f(x,y) \, dA \approx (1)/(2\pi) = (1)/(6.283\pi) \approx 0.01594\]`

Therefore, the average value of
`\(f(x,y) = \sin(x+y)\)` over the given rectangles is approximately:

a) 0.01053

b) 0.01594