Final answer:
After composing the functions f(x) and h(x), we find that the composition does not simplify to x, which indicates that f(x) and h(x) are not inverses of each other; the answer is A. No.
Step-by-step explanation:
To determine if the functions
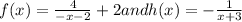
are inverses of each other, we can test if the compositions f(h(x)) and h(f(x)) equal x. We will first calculate f(h(x)).
Substitute h(x) into f(x):
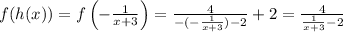
Next, we find a common denominator for the fraction:

As we see, f(h(x)) simplifies to a different expression and does not equal x, therefore f(x) and h(x) are not inverses of each other. So, the answer to the question is A. No, the given functions are not inverses.