Final Answer:
A general solution to the given differential equation
 , where
, where
 are arbitrary constants.
are arbitrary constants.
Step-by-step explanation:
Certainly! To find the general solution to the given differential equation
 we can follow these steps:
we can follow these steps:
1. Assume a Solution:
Assume a solution in the form
 is a constant.
is a constant.
2. Find Derivatives:
Calculate the first and second derivatives of
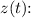
![\[z'(t) = re^(rt), \quad z''(t) = r^2e^(rt)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9ihx5sjwjmzvat5tvld8u3jrax4bdqbtg8.png)
3. Substitute into the Differential Equation:
Substitute
 into the differential equation:
into the differential equation:
![\[2r^2e^(rt) + re^(rt) - 2e^(rt) = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9bndmpwa6k6rmjf7cvwxrk82yryl6xqkr2.png)
4. Factor Out

Factor out the common term

![\[e^(rt)(2r^2 + r - 2) = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xqyo1n56z7hs17n32nj5jbefgjdsdn9qij.png)
5. Set the Expression Inside Parentheses to Zero:
 and solve for
and solve for
 The roots are
The roots are
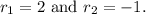
6. Write Down the General Solution:
The general solution is a linear combination of the fundamental solutions corresponding to the roots:
![\[z(t) = C_1 e^(2t) + C_2 e^(-t)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/spjn5cc2aldqyxqyjfjaoe1w54483y7611.png)
This is the general solution to the given differential equation, where
 are arbitrary constants. The solution covers all possible scenarios and initial conditions for the differential equation, providing a versatile representation of the family of solutions.
are arbitrary constants. The solution covers all possible scenarios and initial conditions for the differential equation, providing a versatile representation of the family of solutions.