Question

Solution to two decimal places, if necessary. 3(x+1)² =27

Answer 1

The solution to the given initial value problem
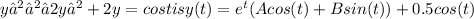`y′′−2y′+2y=cost is y(t) = e^t(Acos(t) + Bsin(t)) + 0.5cos(t)`, where A and B are constants determined by the initial conditions.

Step-by-step explanation:

The given second-order linear differential equation can be solved using the characteristic equation. The characteristic equation for this equation is
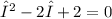`λ^2 - 2λ + 2 = 0`. Solving this quadratic equation, we find that the roots are complex:
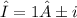`λ = 1 ± i`. This indicates that the general solution will involve sines and cosines.

The complementary solution (homogeneous part) is then
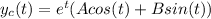`y_c(t) = e^t(Acos(t) + Bsin(t))`, where A and B are arbitrary constants. To find the particular solution (non-homogeneous part) corresponding to the cosine term, we guess a particular solution of the form
`y_p(t) = Ccos(t) + Dsin(t)`. After finding the derivatives and substituting them into the differential equation, we solve for the coefficients C and D.

Combining the complementary and particular solutions, we obtain the general solution:
`y(t) = e^t(Acos(t) + Bsin(t)) + Ccos(t) + Dsin(t)`. Applying the initial conditions will allow us to determine the values of A, B, C, and D. In this case, the particular values of A and B are determined by the initial conditions, and the general solution becomes the specific solution to the given initial value problem.