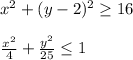Question

Graph the solution to the following x²+(y-2)²>=16 (x²))/(4)+(y²)/(25)<=1

Answer 1

The coordinates of the solution to this system of two equations in two variables are:

x = -1.906 and y = -1.517

x = 1.906 and y = -1.517

In order to graphically determine the solution for this system of equations on a coordinate plane, we would make use of an online graphing calculator to plot the given system of equations while taking note of the point of intersection;

`x^2+(y-2)^2 \geq 16` ......equation 1.

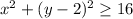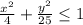`(x^2)/(4) +(y^2)/(25) \leq 1` ......equation 2.

Based on the graph shown, we can logically deduce that the solution for this system of linear equations is the point of intersection of each lines on the graph that represents them in quadrant III and IV. Hence, this is represented by the ordered pairs (-1.906, -1.517) and (1.906, -1.517).

In this context, the pair of linear equation has exactly two solutions;

x = -1.906 and y = -1.517

x = 1.906 and y = -1.517

Complete Question:

Graph the solution to the following;

`x^2+(y-2)^2 \geq 16 \\\\(x^2)/(4) +(y^2)/(25) \leq 1`