Question

Find f"(x) the third derivative of f and f^(4)(x) the fourth derivative of f for each function

f(x)=−2x 4 +7x 3 +4x 2 +x

Answer 1

For the function f(x) =
`-2x^4 + 7x^3 + 4x^2 + x,` the third derivative, f''(x), is f'''(x) = 72x. The fourth derivative,
`f^(4)(x), is f^(4)(x) = 72.`

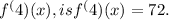
Step-by-step explanation:

Given the function f(x) =
`-2x^4 + 7x^3 + 4x^2 + x`, finding the third derivative involves taking the derivative of the function three times successively. The first derivative, f'(x), of f(x) results in
`f'(x) = -8x^3 + 21x^2`+ 8x + 1. The second derivative, f''(x), is obtained by differentiating f'(x) to get f''(x) =
`-24x^2 + 42x + 8.` Finally, the third derivative, f'''(x), is found by differentiating f''(x) to get f'''(x) = 72x.

Moving on to the fourth derivative, denoted as f^(4)(x), it involves finding the derivative of the third derivative, f'''(x). By taking the derivative of f'''(x) = 72x, the result is a constant value,
`f^(4)(x) = 72`. This signifies that irrespective of the value of x, the fourth derivative of the given function f(x) remains constant at 72. Thus, the third derivative f'''(x) = 72x, while the fourth derivative
`f^(4)(x)` is a constant value of 72, indicating the rate of change at that particular level of differentiation.