Question

A water tank is in the shape of an inverted cone. The radius of the base is 8 meters and the height is 12 meters. The tank is being emptied for cleaning at the rate of 4met³ /minute. Find the rate at which the water level will be decreasing, when the water is 6 meters deep.

Answer 1

When the water level is 6 meters deep, the rate at which the water level will be decreasing is

`4 m^3/`

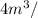
minute.

Step-by-step explanation:

To find the rate at which the water level of the tank is decreasing, we can use the concept of similar triangles. When the water level is 6 meters deep, the height of the smaller cone formed by the remaining water will be 6 meters. Let's call this height h. The radius of the smaller cone can be found using the ratio of the heights of the cones, which is 6/12 = 1/2. So, the radius of the smaller cone is (1/2) * 8 = 4 meters.

Now, we can use the formula for the volume of a cone to find the volume of the smaller cone. The volume of a cone is given by

`V = (1/3) * π * r^2 * h`

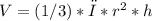
, where V is the volume, π is approximately 3.14, r is the radius, and h is the height. Plugging in the values, we get V =

`(1/3) * 3.14 * 4^2 * 6 = 100.48 m^3.`

Since the water is being emptied at a rate of

`4 m^3/`

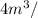
minute, the rate at which the water level will be decreasing is

`4 m^3/`

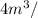
minute.