Question

Rewrite each equation in logarithmic form. 15^(-2)=(1)/(225)

Answer 1

The logarithmic form of the equation
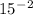`15^-^2` = 1/225 is log₁₅(1/225) = -2.

Step-by-step explanation:

In logarithmic form, the equation
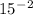`15^-^2` = 1/225 can be expressed as log base 15 of (1/225) equals -2. The base of the logarithm, in this case, is 15. The logarithm is essentially asking the power to which the base (15) must be raised to obtain the result on the other side of the equation (-2). Therefore, log₁₅(1/225) = -2 implies that 15 raised to the power of -2 is equal to 1/225.

To understand this, we can break down the original equation.
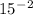`15^-^2` is equivalent to 1 divided by
`15^2`, which is 1/225. The logarithmic form succinctly captures this relationship by expressing the power (-2) as the logarithm base 15 of 1/225. This mathematical notation is a more compact and abstract way of representing the same underlying arithmetic.

Logarithms are valuable in solving equations involving exponents, and they provide a powerful tool for simplifying complex mathematical relationships. In this case, the logarithmic form clarifies the connection between the exponent, base, and result in a concise and systematic manner.