Question

Choose the best option for the system of equations: -2x-2y=16 and -x+y=-4. Which of the following statements is true regarding these two equations?

A) The equations are parallel, and there is no solution.
B) The equations are parallel, and there is a unique solution.
C) The equations are not parallel and have a unique solution.
D) The equations are not parallel and have no solution.

Answer 1

The system of equations
`-2x-2y=16` and
`-x+y=-4` can be rewritten to show they have slopes of
`-1` and
`1`, respectively, meaning they are not parallel and will intersect at one point, indicating a unique solution. Thus, the correct answer is C) The equations are not parallel and have a unique solution.

Step-by-step explanation:

To determine whether the equations are parallel and what type of solution they have, we can compare their slopes.

For the system of equations
`-2x-2y=16` and
`-x+y=-4`, we can rewrite them in slope-intercept form
`(y = mx + b)` to easily find their slopes
`(m)`.

Rewriting the first equation:

Divide all terms by
`-2: x + y = -8`

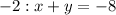
Rewrite as
`y = -x - 8`

Rewriting the second equation:

Multiply by
`-1: x - y = 4`

Rewrite as
`y = x - 4`

The first equation has a slope of
`-1` and the second equation has a slope of
`1`. Since the slopes are not equal, the lines are not parallel. To determine if there is a unique solution, we can see that the two lines have different y-intercepts

(
`-8` and
`-4,` respectively).

Therefore, they will intersect at one point, indicating there is a unique solution.

The correct answer to the question is: C) The equations are not parallel and have a unique solution.