Question

Use the linear approximation to estimate (-0.97)^2 * (2.01)^2 ≈ . Compare with the value given by a calculator and compute the percentage error: Error = %.

Answer 1

To estimate

`(-0.97)^2 * (2.01)^2`

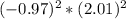
using linear approximation, calculate

`(-0.97)^2`

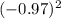
and

`(2.01)^2`

separately, multiply the approximations, and compare with the exact value. The percentage error is computed by subtracting the estimated value from the exact value, dividing by the exact value, and multiplying by 100.

Step-by-step explanation:

To estimate

`(-0.97)^2 * (2.01)^2`

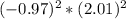
using linear approximation, we start by evaluating

`(-0.97)^2`

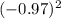
and

`(2.01)^2`

separately.

`(-0.97)^2 ≈ 0.9409 and (2.01)^2 ≈ 4.0401.`

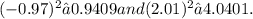
Then we multiply these two approximations to get the estimated value of (-

`0.97)^2 * (2.01)^2,`

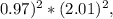
which is approximately 0.9409 * 4.0401 = 3.7993.

Comparing this estimate with the value given by a calculator, we find that the exact value is 0.9409 * 4.0401 = 3.80039009.

To compute the percentage error, we subtract the estimated value from the exact value, divide by the exact value, and multiply by 100. The error is ((3.80039009 - 3.7993) / 3.80039009) * 100 ≈ 0.0288%, rounded to four decimal places.