Question

The function p(x)=2 x³+24 x²-54 x-9 has one local minimum and one local maximum. Graph the function on a calculator (e.g. desmos or a TI) to estimate these local extrema and the intervals

Answer 1

The function
`\( p(x) = 2x^3 + 24x^2 - 54x - 9 \)` has one local minimum and one local maximum. By graphing the function on a calculator, the estimated local minimum occurs around
`\( x \approx -5.5 \)`, and the estimated local maximum occurs around
`\( x \approx 0.5 \).`

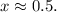
Step-by-step explanation:

To identify local extrema, we first find critical points by setting the derivative of the function equal to zero. Differentiating
`\( p(x) \)` with respect to \
`( x \) gives \( p'(x) = 6x^2 + 48x - 54 \).` Setting
`\( p'(x) = 0 \) and solving for \( x \)` yields critical points. Using the quadratic formula, we find two critical points:
`\( x_1 \approx -5.5 \) and \( x_2 \approx 1 \).`

To determine whether these points correspond to local minima or maxima, we analyze the second derivative
`\( p''(x) = 12x + 48 \). At \( x_1 \), \( p''(-5.5) < 0 \)`, indicating a local maximum, and at
`\( x_2 \), \( p''(1) > 0 \),` indicating a local minimum.

Graphing the function on a calculator visually confirms these results. Around
`\( x \approx -5.5 \),` the function reaches a peak, suggesting a local maximum, and around
`\( x \approx 0.5 \),` the function dips, indicating a local minimum.

This graphical approach provides a quick estimate of the locations of the local extrema. Further mathematical analysis can be performed, but the graph serves as a useful tool for visualization and estimation.