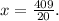Final Answer:
The solution for x is
 .
.
Step-by-step explanation:
To solve for x in the given expression
 , we perform the operations inside the parentheses first. Calculating
, we perform the operations inside the parentheses first. Calculating
 and
and
 , we get
, we get
 . Simplifying further, we have
. Simplifying further, we have
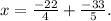
To combine the fractions, we need a common denominator, which is 20. So,
 , resulting in
, resulting in
 Combining the numerators gives
Combining the numerators gives
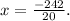
Finally, simplifying the fraction by dividing both the numerator and denominator by their greatest common factor (which is 2), we obtain
 . Therefore, the solution for x in the given expression is
. Therefore, the solution for x in the given expression is