Question

Find the relative maximum value of the function f(x, y)=x² y subject to the constraint x+y=10

Answer 1

The relative maximum value of the function
`\(f(x, y) = x^2 y\)` subject to the constraint
`\(x + y = 10\)` occurs at the point
`\((5, 5)\)` with a maximum value of
`\(125\).`

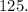
Step-by-step explanation:

Certainly! To find the relative maximum value of the function
`\(f(x, y) = x^2 y\)`subject to the constraint
`\(x + y = 10\),` we can use the method of Lagrange multipliers.

1. Formulating the Lagrangian:

The Lagrangian function is given by:

`\[L(x, y, \lambda) = x^2 y + \lambda(10 - x - y)\]`

2. Taking Partial Derivatives:

Calculate the partial derivatives of
`\(L\) with respect to \(x\), \(y\), and \(\lambda\)` and set them equal to zero:

`\[(\partial L)/(\partial x) = 2xy - \lambda = 0\]`

`\[(\partial L)/(\partial y) = x^2 - \lambda = 0\]`

`\[(\partial L)/(\partial \lambda) = 10 - x - y = 0\]`

3. Solving the System of Equations:

Solve the system of equations to find the critical points. From the first two equations, we get
`\(x = y\) and \(\lambda = x^2\).` Substituting into the third equation
`(\(10 - x - y = 0\)),` we find
`\(x = y = 5\) and \(\lambda = 25\).`

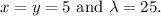
4. Substitute into the Objective Function:

Substitute these values back into the objective function
`\(f(x, y)\):`

`\[f(5, 5) = 5^2 * 5 = 125\]`

Therefore, the relative maximum value of the function
`\(f(x, y) = x^2 y\)`subject to the constraint
`\(x + y = 10\)` occurs at the point
`\((5, 5)\)` with a maximum value of
`\(125\)`. This point satisfies both the original function and the constraint, and the Lagrange multipliers method helps identify critical points for optimization problems with constraints.