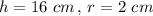Question

Please answer as quickly as you can! ♥ Find two possible dimensions for a cylinder that has a volume of 64π cm³.

Answer 1

Possible dimensions are
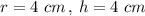`r=4\,\,cm\,,\,h=4\,\,cm` and
`h=16\,\,cm\,,\,r=2\,\,cm`

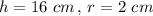
Explanation:

Given:

Volume of a cylinder is
`64\pi\,\,cm^3`

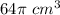
To find: Dimensions of a cylinder

Solution:

Let
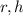`r,h` denote height of a cylinder.

Volume of a cylinder =
`\pi r^2h`

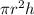
Therefore,

`64\pi=\pi r^2h\\64=r^2h\\4^2\,4=r^2h`

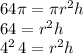
One possible dimension can be
`r=4\,\,cm\,,\,h=4\,\,cm`.

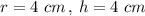Also,
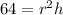`64=r^2h` can be written as
`16(2^2)=hr^2`

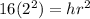
So, another possible dimension can be
`h=16\,\,cm\,,\,r=2\,\,cm`