Final Answer:
a. The curve has vertical tangent lines at
 and ( x = 2 ). b. The curve does not have any horizontal tangent lines.
and ( x = 2 ). b. The curve does not have any horizontal tangent lines.
Step-by-step explanation:
The points where the curve has a vertical tangent line can be found by determining the values of ( x ) for which the derivative of ( y ) with respect to ( x ) is undefined.
Taking the derivative of the given curve ( 7x + 4
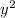 - y = 2 ) with respect to ( x ) and setting it equal to zero, we find the critical points. Solving for ( x ) gives us
- y = 2 ) with respect to ( x ) and setting it equal to zero, we find the critical points. Solving for ( x ) gives us
 and ( x = 2 ), indicating the points where the curve has vertical tangent lines.
and ( x = 2 ), indicating the points where the curve has vertical tangent lines.
To check for horizontal tangent lines, we need to examine the second derivative. If the second derivative is equal to zero, the curve has points with horizontal tangent lines. In this case, since the curve doesn't have any points where the second derivative is zero, there are no horizontal tangent lines.