Question

Find the most general antiderivative of the function. (Check your answer by differentiation. Use C for the constant of the antiderivative.)

f(x)=√(x²)+x √(x)

Answer 1

The antiderivative of the function

`f(x) = \u221a(x\u00b2) + x \u221a(x) is F(x) = \u00bdx\u00b2 + \u00be/\u00b5x\u00b5/\u00b2 + C`

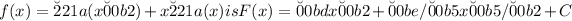
, after correcting the expression \u221a(x\u00b2) to x and applying the power rule for integration to each term.

Step-by-step explanation:

The question asks for the most general antiderivative of the function f(x) = √(x²) + x √(x). To find the antiderivative, we need to first correct the expression √(x²), which is simplified to x, because the square root of x squared is x. Therefore, the function simplifies to f(x) = x + x¹½. Now, to find the antiderivative, we will apply the power rule for integration to each term.

To integrate x, we add 1 to its exponent to get x² and then divide by the new exponent, resulting in ½x². For the term x¹½, we add 1 to ¾ to get xµ/² (x to the 5/2 power) and then divide by 5/2, which is equivalent to multiplying by 2/5, resulting in ¾/µxµ/². Adding a constant C gives us the most general antiderivative.

Finally, we have the antiderivative of f(x) as F(x) = ½x² + ¾/µxµ/² + C. To check our solution, we differentiate F(x) and should obtain the original function f(x).