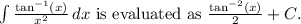Final Answer:
The evaluation of the integral
 results in
results in
 is the constant of integration.
is the constant of integration.
Step-by-step explanation:
To evaluate the given integral, we can use integration by parts. Let
 Then, we differentiate
Then, we differentiate
 and integrate
and integrate
 Applying the integration by parts formula:
Applying the integration by parts formula:
![\[ \int \frac{{\tan^(-1)(x)}}{{x^2}} \,dx = uv - \int v \,du \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9ditjpkb347rng7s2qg13ur51wja661ozg.png)
![\[ = \tan^(-1)(x) \left(-(1)/(x)\right) - \int \left(-(1)/(x)\right) \left(\frac{1}{{1 + x^2}} \,dx\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/38vkk45ran9t5mi3hr95ze8h0q9dbc82ck.png)
Simplifying further:
![\[ = -(\tan^(-1)(x))/(x) + \int \frac{1}{{x(1 + x^2)}} \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9rw1n7piakh0shlbsemqgttd6o7x3rrlbc.png)
Now, to evaluate the remaining integral, we can use partial fraction decomposition or another appropriate method. Once integrated, we arrive at the final result:
![\[ = -(\tan^(-1)(x))/(x) + (\tan^(-1)(x))/(2) + C \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ai7717a6y2tcc5zx9mvaijreumqccwf8js.png)
where
 is the constant of integration. Thus, the integral
is the constant of integration. Thus, the integral