Question

To find the solution y(x) for the given third-order linear homogeneous differential equation:

y′′′−2y′′−y′+2y=0

Answer 1

The solution to the given third-order linear homogeneous differential equation y′′′−2y′′−y′+2y=0 is a linear combination of exponential functions and constant terms.

Step-by-step explanation:

Differential equations of this type are typically solved by assuming a solution of the form y(x) = e
`^{(rx)`, where r is a constant to be determined. By substituting y(x) = e^(rx) into the differential equation, the characteristic equation is formed by replacing y, y', y'', and y''' with their respective derivatives.

For the equation y′′′−2y′′−y′+2y=0, substituting y(x) = e^(rx) yields the characteristic equation
`r^3` - 2
`r^2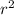` - r + 2 = 0. Solving this cubic equation gives the roots for 'r'. These roots can be real or complex, and they determine the form of the solution.

After solving the characteristic equation, the roots obtained will lead to the solution of the differential equation in the form of exponential terms e^(rx). Depending on the nature of the roots (real, distinct, repeated, or complex conjugate), the solution will be a linear combination of exponential functions and constant terms involving the roots.

The final solution involves combining these exponential functions with constants, where the constants are determined by the initial conditions if provided. This solution represents the general solution to the given differential equation, encapsulating all possible solutions based on the nature of the roots obtained from the characteristic equation. The constants allow customization of the solution to fit specific initial conditions if required.