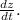Final Answer:
The expression for
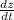 using the Chain Rule is
using the Chain Rule is
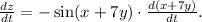 Substituting the given values and their derivatives, we get
Substituting the given values and their derivatives, we get
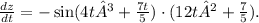
Step-by-step explanation:
To find
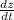 using the Chain Rule, we begin by expressing z as a composite function of t. In this case, (z = cos(x + 7y), where (x = 4t³) and
using the Chain Rule, we begin by expressing z as a composite function of t. In this case, (z = cos(x + 7y), where (x = 4t³) and
 ). The Chain Rule states that
). The Chain Rule states that
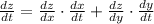 . In this context
. In this context

 is
is
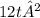 ,
,
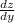 is
is
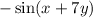 , and
, and
 is
is

Substituting these values into the Chain Rule formula, we ge
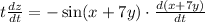 . Expanding further and substituting the derivatives of\(x) and (y), we arrive at the final expression
. Expanding further and substituting the derivatives of\(x) and (y), we arrive at the final expression
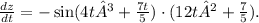
In conclusion, the application of the Chain Rule allows us to find the rate of change
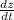 with respect to (t) in a composite function involving z, x, and y. The detailed calculation involves systematically applying the Chain Rule to each component, resulting in the final expression for
with respect to (t) in a composite function involving z, x, and y. The detailed calculation involves systematically applying the Chain Rule to each component, resulting in the final expression for