Question

Evaluate The Following.
A. ∫(X²+1)2dx
B. ∫X−X²dx

Answer 1

To evaluate the given integrals, we need to expand the binomial and integrate term by term for the first integral, and directly integrate each term for the second integral. The results, including the constant of integration, are given for both integrals.

Step-by-step explanation:

To evaluate the integrals ∫(X²+1)²dx and ∫X-X²dx, we will perform integration separately for each term.

Integral A

For the first integral, we expand the integrand:

`(X² + 1)² = X⁴ + 2X² + 1`

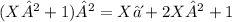
Then perform the integral term by term:

`∫X⁴ dx = ⅓ X⁵∫2X² dx = ⅓ X³∫1 dx = X`

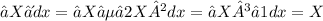
Combine these to get the antiderivative, plus the constant of integration C:

⅓ X⁵ + ⅓ X³ + X + C

Integral B

For the second integral, we simply perform the integral for each term:

∫X dx = ½ X²

- ∫X² dx = -⅓ X³

Combine these to get the antiderivative, plus the constant of integration C:

½ X² - ⅓ X³ + C

Integration is a fundamental concept in calculus used to find the area under a curve or to solve differential equations, among other applications. The result of integration is the antiderivative or the integral of the function, with an arbitrary constant C included since indefinite integrals do not specify limits of integration.