Question

Find The Area Of The Region Bounded By The Curves: Y=X2+2x And Y=−X+4

Answer 1

To calculate the area between the curves
`y = x^2 + 2x` and
`y = -x + 4`, find their points of intersection, and integrate the difference of the two functions over the interval defined by these intersection points.

Step-by-step explanation:

To find the area of the region bounded by the curves
`y = x2 + 2x`

and
`y = -x + 4`, we first need to determine the points of intersection by setting the two equations equal:

`x2 + 2x = -x + 4`

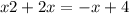
Solving this quadratic equation will give us the
`x`-values where the curves intersect.

Next, we integrate the difference between the two functions over the interval defined by these points of intersection.

We integrate
`y = (-x + 4) - (x2 + 2x)` from the smaller
`x`-value to the greater x-value. This integration calculates the area directly, and it's important to consider the absolute value if the top function becomes the bottom function over the interval.The integral yields the area of the region we are looking for.