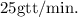Final Answer:
The rate of infusion for (D5W) at
 with a drop factor of
with a drop factor of
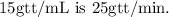
Step-by-step explanation:
To determine the drops per minute
 you can use the formula:
you can use the formula:
![\[\text{{Drops per minute}} = \left( \frac{{\text{{Volume per hour}}}}{{\text{{Drop factor}}}} \right) * (1)/(60)\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/oovj96950n946xk6f1j839lqmssozwzl0e.png)
In this case, the volume per hour is
 and the drop factor is
and the drop factor is
 . Plug these values into the formula:
. Plug these values into the formula:
![\[\text{{Drops per minute}} = \left( \frac{{125}}{{15}} \right) * (1)/(60)\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/n10aqahp02y2r7pg9d2cxw0nmmfuotpo0w.png)
Now, calculate the drops per minute:
![\[\text{{Drops per minute}} = \left( \frac{{25}}{{3}} \right) * (1)/(60) = (25)/(180) * (1)/(60) = (25)/(10,800)\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/k5pt6g5vq0q7jikwntod0hc6fly6vci1rr.png)
Simplify the fraction:
![\[\text{{Drops per minute}} = (5)/(2,160)\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/ik07y6inmw6e26m2d2vprq83dkccyf3rs3.png)
To express this in a more practical form, convert this fraction to a decimal:
![\[\text{{Drops per minute}} \approx 0.00231\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/nb5zjvjekn65km3aorx36r7lqymi2adx9r.png)
Finally, convert the decimal to a whole number by multiplying by 60:
![\[\text{{Drops per minute}} \approx 0.00231 * 60 \approx 0.1386 \approx 0.14\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/v8wpc0dnvzhuyhfgtmj00b79wum8btyskf.png)
Therefore, the drops per minute is approximately (0.14) or