Question

How do I find the answer

Answer 1

The function
`\( f(x) = \log(\log(x)) \)` has
`\( f^(-1)(x) = 3^(2x) \)` is the correct choice.

The given function is
`\( f(x) = \log(\log(x)) \)`, and we are tasked with finding its inverse, denoted as
`\( f^(-1)(x) \).`

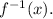
To determine the inverse, switch the roles of \( x \) and \( f(x) \) and solve for \( x \).

Begin with the original function:

`\[ y = \log(\log(x)) \]`

Interchange \( x \) and \( y \):

`\[ x = \log(\log(y)) \]`

Now, eliminate the outer logarithm by exponentiating both sides:

`\[ 10^x = \log(y) \]`

Again, eliminate the remaining logarithm:

`\[ y = 10^(10^x) \]`

Now, this can be expressed in the form
`\( f^(-1)(x) \)`.

Comparing the options, we find that the correct expression for
`\( f^(-1)(x) \)`is:

`\[ \text{B. } 3^(2x) \]`

Thus,
`\( f^(-1)(x) = 3^(2x) \)` is the correct choice.

The probable question may be:

The function f is given by f(x) = log(log, x). Which of the following is an expression for f-1(x)?

A. 2^{3x}

B. 3^{2x}

C.2\cdot3^x

D. 3 \cdot2^x