Question

The table gives the amount of debt, in dollars, on an individual's credit card for certain months after opening the credit card. Using an exponential regression y=ab^x to model these data, what is the debt at month 24 predicted by the exponential function model, to the nearest dollar? (

Answer 1

The answer is (C) 42,159.

Determine the exponential model:

The general form for an exponential model is y = ab^x, where a is the initial value, b is the growth factor, and x is the time (in months in this case).

We'll need to use the given data points to find the values of a and b.

Solve for a and b:

Using the point (1, 620): 620 = ab^1, so a = 620.

Using the point (4, 1083): 1083 = 620b^4, so b^4 ≈ 1.747, and b ≈ 1.154.

Predict the debt in the 12th month:

Now that we have the model y = 620(1.154)^x, we can plug in x = 12 to find the predicted debt:

y = 620(1.154)^12 ≈ 42,159

Round to the nearest dollar:

The predicted debt in the 12th month, to the nearest dollar, is 42,159.

Complete Question:

`\begin{array}{cc}\text { Month}({x}) & {Debt}({y}) \text {(dollars) } \\1 & 620 \\4 & 1,083 \\5 & 1,215 \\7 & 1,902\end{array}`

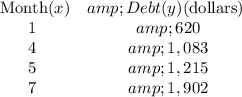
The exponential function model, to the nearest dollar? (Assume that the debt continues and that no payments are made to reduce the debt.)

(A) 5,267

(B) 15,187

(C) 42,159

(D) 1,972,745

Answer 2

The exponential function which models the data is :
`y= 514.822(1.2043)^(x)` and the debt after 24 months is 44595. Hence , the most appropriate option is C

Expressing the exponential equation in the form ;
`y = ab^x`

Using the pair of points;

• (1, 620) ; (4, 1083)

Using (1, 620) to solve for a ;

`620 = a(b)^(1)` ____(1)

Using the other point (4, 1083) to solve for b:

`1083 = a(b)^(4)` ____(2)

Dividing equation (2) by (1) :

`1.7468 = (b)^(3)`

b = 1.2043

Substituting this value of b to get a

`620 = a(1.2043)^(1)` ____(1)

620 = 1.2043a

a = 620/1.2043

a = 514.822

Hence, the equation becomes :
`y= 514.822(1.2043)^(x)`

B.)

At month 24 ;

• x = 24

`y = 514.822(1.2043)^(24)`

y ≈ 44595