Question

Range of f(x) = 3x^2-4x+5) is

Answer 1

The range of the function

`f(x) = 3x^2 - 4x + 5`

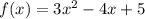
is determined by its vertex, which represents the minimum value of the function since the parabola opens upwards. The vertex occurs at x = 2/3, and by substituting this back into the function, we find that the minimum value is 11/3. Hence, the range is all real numbers greater than or equal to 11/3.

Step-by-step explanation:

The question asks for the range of the quadratic function

`f(x) = 3x^2 - 4x + 5`

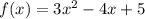
. To find the range, we need to identify the minimum value of the function since it is a parabola that opens upwards (the coefficient of

`x^2`

is positive).

First, we can find the vertex of the parabola, which will give us the minimum point of the function. The vertex formula in terms of x is given by x = -b/(2a). Plugging in the values from the quadratic function (a = 3, b = -4), we get x = -(-4)/(2*3) = 4/6 = 2/3.

Inserting x = 2/3 into the function, we obtain the minimum value

`f(2/3) = 3*(2/3)^2 - 4*(2/3) + 5`

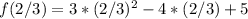
. Calculating this, we get

`f(2/3) = 3*(4/9) - 8/3 + 5 = 4/3 - 8/3 + 5 = 4 - 8/3 + 15/3 = 11/3.`

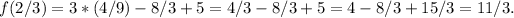
Therefore, the range of f(x) is all real numbers greater than or equal to 11/3.