Final answer:
The domain of the function f(x) = 1/(x^2 - 4) is all real numbers except for x = 2 and x = -2, where the function is undefined due to division by zero.
Step-by-step explanation:
The domain of the function
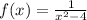
is the set of all real numbers except for the values that make the denominator equal to zero. To find these values, we set the denominator equal to zero and solve for x:
![\[x^2 - 4 = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ffqj77185xso3bsb1yjeclun141jlgbs5y.png)
Solving this equation gives us:
![\[x^2 = 4\]\\\x = \pm 2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kdmls1lq0mn0jt7i9usfovz3jgz04h5080.png)
The domain of f(x) is all real numbers except x = 2 and x = -2, because at these points the denominator would be zero, which is not allowed as it would make the function undefined.