Question

Thank you so much for the help!

Answer 1

The equations of the line are
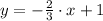`y = - (2)/(3)\cdot x + 1` and
`y = - 7 \cdot x + 2`.

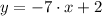How to determine the equation of a line

In this problem we must determine two line equations based on information available on graph. Lines are modelled after the following expression:

y = m · x + b

Where:

• x - Independent variable.
• y - Dependent variable.
• m - Slope
• b - Intercept

Slope can be found by means of secant line formula:

`m = (\Delta y)/(\Delta x)`

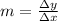
Where:

• Δx - Change in independent variable.
• Δy - Change in dependent variable.

And intercept of the line is the point that is on y-axis.

Now we proceed to determine the equation of the line:

Case 1:

Slope:

`m = (- 1 - 3)/(3 - (- 3))`

`m = - (2)/(3)`

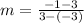
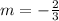
Intercept:

b = y - m · x

b = 1 - m · 0

b = 1

The equation of the line is
`y = - (2)/(3)\cdot x + 1`.

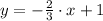Case 2:

Slope:

`m = (- 5 - 2)/(1 - 0)`

m = - 7

Intercept:

b = y - m · x

b = 2 - m · 0

b = 2

The equation of the line is
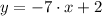`y = - 7 \cdot x + 2`.