Question

1. What is the value of h in the figure
below?

Answer 1

The value of h is
`\(6 √(5)\).`

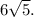
Since YO is perpendicular to side XZ in triangle XYZ, we can use the Pythagorean theorem to find the length of YO.

The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

In this case, YO is the hypotenuse, and XO and OZ are the other two sides.

`\[ YO^2 = XO^2 + OZ^2 \]`

`\[ h^2 = 12^2 + 6^2 \]`

`\[ h^2 = 144 + 36 \]`

`\[ h^2 = 180 \]`

`\[ h = √(180) \]`

`\[ h = 6 √(5) \]`

So, the value of h is
`\(6 √(5)\).`

The probable question may be:

In triangle XYZ, YO is perpendicular to side XZ, XO=12 OZ=6, YO=h

What is the value of h in the figure below?