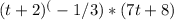Question

Factor the following expression. Simplify your answer. 3t(t+2)^(-(1)/(3))+4(t+2)^((2)/(3))

Answer 1

To factor the expression

`3t(t+2)^(-1/3) + 4(t+2)^(2/3)`

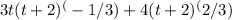
, factor out the common term

`(t+2)^(-1/3) to get (t+2)^(-1/3) * (7t + 8).`

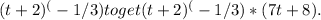
Step-by-step explanation:

The student is asking to factor the expression

`3t(t+2)^(-1/3) + 4(t+2)^(2/3)`

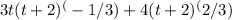
. To factor this expression, we can look for a common factor in both terms. Both terms have a factor of (t+2) raised to a power, though the powers are different. We can factor out the smallest power of (t+2), which is

`(t+2)^(-1/3).`

When we factor out

`(t+2)^(-1/3)`

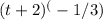
, we are left with the expression:

`(t+2)^(-1/3) * (3t + 4(t+2))`

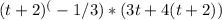
To simplify further, we multiply the 4 by (t+2) inside the parentheses:

`(t+2)^(-1/3) * (3t + 4t + 8)`

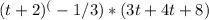
Combine like terms:

`(t+2)^(-1/3) * (7t + 8)`