Question

Find the dimensions of a rectangle with an area of 16 square feet that has the minimum perimeter The dimensions of this rectangle are it.

Answer 1

The dimensions of a rectangle with an area of 16 square feet that has the minimum perimeter is a square with side lengths of
`4` feet each, making the dimensions
`4` feet by
`4` feet.

Step-by-step explanation:

To find the dimensions of a rectangle with an area of 16 square feet that has the minimum perimeter, we can utilize the properties of rectangles. The rectangle with the smallest perimeter for a given area is a square. This is because the square has equal sides and the sum of its side lengths (perimeter) for a given area is the least compared to any other rectangle with the same area.

The area of a rectangle is calculated using the formula:

`Area = length × width`

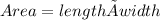
Since we are looking for a square:

`Area = side × side`

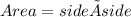
If the area is 16 square feet, and both sides are equal, we can write:

`side × side = 16`

`side2 = 16`

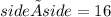
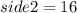
To find the side length, take the square root of both sides:

`side = √16`

`side = 4 feet`

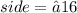
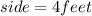
Therefore, the dimensions of the square (which is a special case of a rectangle) with an area of
`16` square feet and the minimum perimeter are
`4` feet by
`4` feet.