Question

NO LINKS!! Please help me with this sequence Part 1x​

Answer 1

1.

s₁ = 2

s₂ = 3

s₃ = 4

s₄ = 9

s₅ = 32

s₆ = 279

s₇ = 8,896

s₈ = 2,481,705

s₉ = 22,077,238,784

2. 2,490,930

3. Neither.

4. 121,800

Explanation:

Question 1

A recursive rule for a sequence allows you to find the nth term of the sequence provided you know the value of the previous term in the sequence.

Given recursive rule:

`\begin{cases}s_n=s_(n-2) \cdot (s_(n-1)-1)\\s_1=2\\s_2=3\end{cases}`

Therefore, the first 9 terms of the sequence are:

`s_1=2`

`s_2=3`

`\begin{aligned}s_3&=s_(3-2) \cdot (s_(3-1)-1)\\&=s_(1) \cdot (s_(2)-1)\\&=2 \cdot (3-1)\\&=2 \cdot 2\\&=4 \end{aligned}`

`\begin{aligned}s_4&=s_(4-2) \cdot (s_(4-1)-1)\\&=s_(2) \cdot (s_(3)-1)\\&=3 \cdot (4-1)\\&=3 \cdot 3\\&=9 \end{aligned}`

`\begin{aligned}s_5&=s_(5-2) \cdot (s_(5-1)-1)\\&=s_(3) \cdot (s_(4)-1)\\&=4 \cdot (9-1)\\&=4 \cdot 8\\&=32 \end{aligned}`

`\begin{aligned}s_6&=s_(6-2) \cdot (s_(6-1)-1)\\&=s_(4) \cdot (s_(5)-1)\\&=9 \cdot (32-1)\\&=9 \cdot 31\\&=279\end{aligned}`

`\begin{aligned}s_7&=s_(7-2) \cdot (s_(7-1)-1)\\&=s_(5) \cdot (s_(6)-1)\\&=32 \cdot (279-1)\\&=32 \cdot 278\\&=8896\end{aligned}`

`\begin{aligned}s_8&=s_(8-2) \cdot (s_(8-1)-1)\\&=s_(6) \cdot (s_(5)-1)\\&=279 \cdot (8896-1)\\&=279\cdot 8895\\&=2481705\end{aligned}`

`\begin{aligned}s_9&=s_(9-2) \cdot (s_(9-1)-1)\\&=s_(7) \cdot (s_(8)-1)\\&=8896\cdot (2481705-1)\\&=8896\cdot 2481704\\&=22077238784\end{aligned}`

Question 2

Given series:

`\displaystyle \sum^8_(k=1) s_k`

The sum notation asks to find the sum of the first 8 terms of the sequence from question 1.

Therefore:

`\begin{aligned}\displaystyle \sum^8_(k=1) s_k&=s_1+s_2+s_3+s_4+s_5+s_6+s_7+s_8\\&=2+3+4+9+32+279+8896+2481705\\&=2490930\end{aligned}`

Question 3

If a sequence is arithmetic, the difference between consecutive terms is the same (this is called the common difference).

If a sequence is geometric, the ratio between consecutive terms is the same (this is called the common ratio).

As the difference between consecutive terms it not the same, the sequence is not arithmetic.

As the ratio between consecutive terms is not the same, the sequence is not geometric.

Therefore, the sequence is neither arithmetic nor geometric.

Question 4

`\boxed{\begin{minipage}{7.3 cm}\underline{Sum of the first $n$ terms of an arithmetic series}\\\\$S_n=(1)/(2)n[2a+(n-1)d]$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the first term. \\ \phantom{ww}$\bullet$ $d$ is the common difference.\\ \phantom{ww}$\bullet$ $n$ is the position of the term.\\\end{minipage}}`

Given arithmetic sequence:

• 12, 18, 24, ...

Therefore:

• a = 12
• d = 18 - 12 = 6

To find the sum of the first 200 terms, substitute the found values of a and d into the formula along with n = 200:

`\begin{aligned}S_(200)&=(1)/(2)(200)[2(12)+(200-1)(6)]\\&=100[24+(199)(6)]\\&=100[24+1194]\\&=100[1218]\\&=121800\end{aligned}`

Answer 2

1. 2, 3, 4, 9, 32, 279, 8896, 2481705, 22077238784
2. 2,490,930
3. neither
4. 121,800

Explanation:

1. Recursively-defined sequence

You want the first 9 terms of the recursive sequence defined by ...

`\begin{cases}s_1=2\\s_2=3\\s_n=s_(n-2)(s_(n-1)-1)\end{cases}`

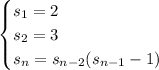
The attached spreadsheet uses the given formula for the next term. It shows the terms to be ...

2, 3, 4, 9, 32, 279, 8896, 2481705, 22077238784

2. Sequence sum

The attached spreadsheet sum function has been used to find the sum of the first 8 terms. That sum is ...

2490930

3. Sequence type

The sequence of problem 1 has neither a common difference nor a common ratio between successive terms. It is neither arithmetic nor geometric.

4. Sum of arithmetic sequence

The sum of the first n terms of an arithmetic sequence with first term a1 and common difference d is given by ...

Sn = (2a1 +d(n -1))(n/2)

You have a sequence with a1 = 12 and d = (18-12) = 6. You want the sum of the first 200 terms.

S200 = (2·12 +6(200 -1))(200/2) = 121,800

The sum is 121,800.

__

Additional comment

A spreadsheet is a nice tool for finding terms of a recursively-defined sequence. The formula can include as many terms as necessary, and it can be replicated thousands of times, if necessary. The limitation is that arithmetic is generally limited to 16 significant figures, or so.