a) The claim is generally represented by \(H_₀\), which states that the distribution is uniform.
b) The correct rejection region is:
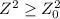
(a) **State H₀ and Hₐ and Identify the Claim:**
 : The distribution of educational attainment responses is uniform among mothers receiving food stamps.
: The distribution of educational attainment responses is uniform among mothers receiving food stamps.
Hₐ: The distribution of educational attainment responses is not uniform among mothers receiving food stamps.
The claim is generally represented by \(H_₀\), which states that the distribution is uniform.
a.

(b) **Determine the Critical Value,
 , and the Rejection Region:**
, and the Rejection Region:**
Given that the significance level
 is 0.01, you need to find the critical value
is 0.01, you need to find the critical value
 from the chi-square distribution table with degrees of freedom df = k - 1, where k is the number of categories.
from the chi-square distribution table with degrees of freedom df = k - 1, where k is the number of categories.
In this case, k = 3, so df = 2
After finding
 , the correct rejection region is:
, the correct rejection region is:
C.
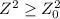
So, the decision rule would be to reject the null hypothesis
 if the calculated chi-square test statistic
if the calculated chi-square test statistic
 is greater than or equal to the critical value
is greater than or equal to the critical value
 , indicating evidence against the claim of a uniform distribution of educational attainment among mothers receiving food stamps.
, indicating evidence against the claim of a uniform distribution of educational attainment among mothers receiving food stamps.
The probable question may be:
A social service organization reports that the level of educational attainment of mothers receiving food stamps is uniformly distributed. To test this claim, you randomly select 96 mothers who currently receive food stamps and record the educational attainment of each. The results are shown in the table on the right. At a 0.01, can you reject the claim that the distribution is uniform? Complete parts (a) through (d) below.
Response Frequency f
Not a high school graduate 37
high school graduate 39
collage (1 year or more) 24
(a) State H_0 and H_a and identify the claim.
H_0: The distribution of educational attainment responses is
H_a: The distribution of educational attainment responses is
Which hypothesis is the claim?
a. H_0
b. H_a
(b) Determine the critical value, 7, and the rejection region.
Z_0^2=
Choose the correct rejection region below.
A. Z^2<Z_0^2
B. Z^2>Z_0^2
C. Z^2<=Z_0^2
D. Z^2<=Z_0^2