Question

In reaching her destination, a backpacker walks with an average velocity of 1.19 m/s, due west. This average velocity results because she hikes for 5.96 km with an average velocity of 3.10 m/s, due west, turns around, and hikes with an average velocity of 0.744 m/s, due east. How far east did she walk

Answer 1

x₂ = 4.455 m

Step-by-step explanation:

The average speed is defined as the displacement traveled between the time interval

v_average =
`(\Delta x)/(\Delta t)`

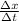
in this case we have a first stop walking west at speed v = 3.10 m / s a ​​distance of x = 5.96 km = 5.96 10³ m

Let's find the time it takes on this tour

v = x / t

t = x / v

t₁ = 5.96 10³ / 3.10

t₁ = 1.9226 10³ s

in a second to walk east at a speed of v₂ = 0.744 m / s

v₂ = x₂ / t₂

t₂ = x₂ / v₂

for full movement

let's assume that the eastward movement is positive

v =
`(- x_1 + x_2)/(t_1 +t_2)`

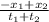
v =
`(-x_1 +x_2)/(t_1 + (x_2)/(t_2) )`

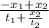
the only unknown term is the distance to the east. We replace and resolve

1.19 =
`(-5.96 \ 10^3 + x_2)/(1.92 \ 10^3 + (x_2)/(0.744) )`

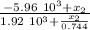
1.19 (1.92 10³ +
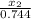`(x_2)/(0.744)`) = x₂ 1.92 10³ - 5.96 10³

2.2848 10³ + 1.599 x₂ = 1.92 10³ x₂ - 5.96 10³

x₂ (1.92 10³ - 1.599) = 2.2848 10³ + 5.96 10³

x₂ = 8.5448 10³ / 1.918 10³

x₂ = 4.455 m