Question

10.42 Teenagers (age 15 to 20) make up 7% of the driving population. The article “More States Demand Teens Pass Rigorous Driving Tests” (San Luis Obispo Tribune, January 27, 2000) described a study of auto accidents conducted by the Insurance Institute for Highway Safety. The Institute found that 14% of the accidents studied involved teenage drivers. Suppose that this percentage was based on examining records from 500 randomly selected accidents. Does the study provide convincing evidence that the proportion of accidents involving teenage drivers differs from .07, the proportion of teens in the driving population?

Answer 1

Based on the study's results, there is convincing evidence to suggest that the proportion of accidents involving teenage drivers differs from 0.07, the proportion of teens in the driving population.

How to determine if the study provides convincing evidence

To determine if the study provides convincing evidence that the proportion of accidents involving teenage drivers differs from 0.07 (the proportion of teens in the driving population), perform a hypothesis test.

Hypotheses:

H₀: The proportion of accidents involving teenage drivers is equal to 0.07.

Ha: The proportion of accidents involving teenage drivers differs from 0.07.

Significance level α = 0.05

We are given that the study examined records from 500 randomly selected accidents, and 14% of those accidents involved teenage drivers. This corresponds to 0.14 * 500 = 70 accidents involving teenage drivers.

To perform the hypothesis test, use the z-test for proportions.

The test statistic formula is:

`z = (\hat{p} - p_0) / \sqrt(p_0(1 - p_0) / n)`

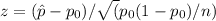
Where:

`\hat{p}` is the sample proportion (70/500 = 0.14)

p₀ is the hypothesized population proportion (0.07)

n is the sample size (500)

Calculating the test statistic:

z = (0.14 - 0.07) /
`\sqrt`(0.07 * 0.93 / 500)

z = 0.07 /
`\sqrt`(0.0651 / 500)

z = 0.07 / 0.0114

z ≈ 6.14

The calculated test statistic is approximately 6.14.

Next, compare the test statistic with the critical value from the standard normal distribution at the given significance level (α = 0.05).

The critical value for a two-tailed test at α = 0.05 is approximately ±1.96.

Since the calculated test statistic (6.14) is greater than the critical value (1.96), we can reject the null hypothesis.

Therefore, based on the study's results, there is convincing evidence to suggest that the proportion of accidents involving teenage drivers differs from 0.07, the proportion of teens in the driving population.