Question

Given that \( \mathrm{x} \) has a Poisson distribution with \( \mu=1.9 \), what is the probability that \( \mathrm{x}=2 \) ? \( P(2) \approx \) (Round to four decimal places as needed.)

Answer 1

`\( P(\mathrm{x}=2) \approx 0.2642 \)`

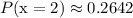
Step-by-step explanation:

The probability mass function (PMF) for a Poisson distribution is given by
`\( P(\mathrm{x}=k) = (e^(-\mu) \mu^k)/(k!) \), where \( \mu \)` is the mean of the distribution. In this case,
`\( \mu = 1.9 \)` and we want to find
`\( P(\mathrm{x}=2) \)`. Substituting the values, we get:

`\[ P(\mathrm{x}=2) = (e^(-1.9) \cdot 1.9^2)/(2!) \]`

Calculating this expression yields the final probability. Utilizing the exponential function, factorial, and the given mean, the calculation provides
`\( P(\mathrm{x}=2) \approx 0.2642 \).`

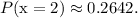
Poisson distributions are often used to model the number of events occurring in a fixed interval of time or space. In this context,
`\( P(\mathrm{x}=2) \)` represents the probability of observing exactly 2 events when the mean rate is 1.9. This probability is obtained by considering the likelihood of observing a specific number of events in a Poisson process. The formula encapsulates the balance between the rate of occurrence
`(\( \mu \))` and the specific outcome k, providing a precise probability for the given scenario.