Question

The depth of the water at the end of the Cocoa Beach Pier varies with the tide on any given day. Suppose the high tide occurs at 5:00 a.m. and the depth of the water is 15.0 feet, then low tide occurs at 11:30 a.m. with a depth of 9.0 feet. Sketch a graph showing how the depth of the water depends on the time, t, in hours, since midnight, t=0.

Answer 1

The sketch of the graph showing the depth of the water at midnight when t = 0 can be seen in the image attached below.

Graphical representation of a function.

A graph can be use to represent a function to make some logical deduction. Here, we can represent the word problem into a piecewise function. To sketch a graph illustrating the depth of the water relies on the time since it range between the low tide and the high tide.

Let denote some of the following parameters;

• time of the high tide (h) = 5:00 am
• time of low tide (l) = 11:30 am
• At high tide, depth of water (H) 15.0 ft
• At low tide, depth of water (L) = 9.0 ft

Representing the parameters in piecewise function, we can have a function D(t) i.e. the function of the depth in terms of time;

`D(t) =\left \{ {{H \ if \ 0 \leq t \leq h} \atop {L \ if \ h \leq t \leq l}} \right.`

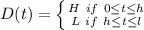
Replacing the values;

`D(t) =\left \{ {{15.0 \ if \ 0 \leq t \leq 5} \atop {9.0 \ if \ 5 \leq t \leq 11.5}} \right.`

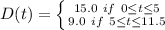
Thus, the sketch of the graph showing the depth of the water at midnight when t = 0 can be seen in the image attached below.