Question

Choose 5 cards from a full deck of 52 cards with 13values (2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K, A) and 4 kinds(spade, diamond, heart, and club). Count how many possible ways to geta(a)Two-pairs: Two pairs plus another card of a different value, for example:(b)Flush: five cards of the same suitbutdifferent values, for example: (c)Full house: A three of a kind and a pair, for example: (d)Four of a kind: Four cards of the same value, for example:

Answer 1

a) 182 possible ways.

b) 5148 possible ways.

c) 1378 possible ways.

d) 2899 possible ways.

Explanation:

The order in which the cards are chosen is not important, which means that we use the combinations formula to solve this question.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

In this question, we have that:

There are 52 total cards, of which:

13 are spades.

13 are diamonds.

13 are hearts.

13 are clubs.

(a)Two-pairs: Two pairs plus another card of a different value, for example:

2 pairs of 2 from sets os 13.

1 other card, from a set of 26(whichever two cards were not chosen above). So

`T = 2C_(13,2) + C_(26,1) = 2*(13!)/(2!11!) + (26!)/(1!25!) = 182`

So 182 possible ways.

(b)Flush: five cards of the same suit but different values, for example:

4 combinations of 5 from a set of 13(can be all spades, all diamonds, and hearts or all clubs). So

`T = 4*C_(13,5) = 4*(13!)/(5!8!) = 5148`

So 5148 possible ways.

(c)Full house: A three of a kind and a pair, for example:

4 combinations of 3 from a set of 13(three of a kind ,c an be all possible kinds).

3 combinations of 2 from a set of 13(the pair, cant be the kind chosen for the trio, so 3 combinations). So

`T = 4*C_(13,3) + 3*C_(13.2) = 4*(13!)/(3!10!) + 3*(13!)/(2!11!) = 1378`

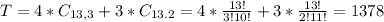
So 1378 possible ways.

(d)Four of a kind: Four cards of the same value, for example:

4 combinations of 4 from a set of 13(four of a kind, can be all spades, all diamonds, and hearts or all clubs).

1 from the remaining 39(do not involve the kind chosen above). So

`T = 4*C_(13,4) + C_(39,1) = 4*(13!)/(4!9!) + (39!)/(1!38!) = 2899`

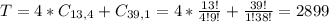
So 2899 possible ways.