Question

A water tank has a square base of area 5 square meters. Initially the tank contains 70 cubic meters. Water leaves the tank, starting at t=0, at the rate of 2 + 4 t cubic meters per hour. Here t is the time in hours. What is the depth of water remaining in the tank after 3 hours

Answer 1

`9.2\ \text{m}`

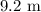
Explanation:

`b` = Surface area of base = 5 square meters

Volume of water in tank = 70 cubic meters

The rate at which the volume is reducing is

`(dV)/(dt)=2+4t\\\Rightarrow dV=2+4tdt`

Integrating from
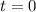`t=0` to
`t=3`

`V=\int^3_0(2+4t)dt\\\Rightarrow V=2t+2t^2|_0^3\\\Rightarrow V=2* 3+2* 3^2-0\\\Rightarrow V=24`

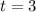
Volume of water remaining in the tank is
`70-24=46\ \text{m}^3`

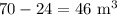
Suface area of base
`*` depth = Volume

`5* d=46\\\Rightarrow d=(46)/(5)\\\Rightarrow d=9.2\ \text{m}`

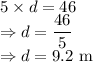
The depth of the water remaining in the tank is
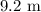`9.2\ \text{m}`.