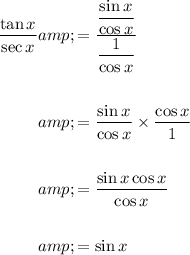Question

Verify that the trigonometric equation is an identity. show all work.

tan x/sec x = sin x

Answer 1

See below.

Explanation:

To verify that tan(x) / sec(x) = sin(x), we can use the following trigonometric identities:

`\boxed{\begin{array}c\underline{\textsf{Quotient identity}}&\underline{\textsf{Reciprocal identity}}\\\\ \tan x = (\sin x)/(\cos x) & \sec x=(1)/(\cos x)\end{array}}`

Begin by substituting the quotient and reciprocal identities:

`(\tan x)/(\sec x)=((\sin x)/(\cos x))/((1)/(\cos x))`

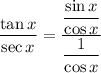
To divide fractions, invert the divisor and multiply it with the dividend:

`=(\sin x)/(\cos x) * (\cos x)/(1)`

`\textsf{Apply the fraction rule:} \quad (a)/(c)* (b)/(d)=(ab)/(cd)`

`=(\sin x\cos x)/(\cos x)`

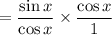
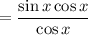
Cancel the common factor cos(x):

`=\sin x`

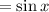
Hence, the given trigonometric equation has been proved.

`\hrulefill`

As one calculation:

`\begin{aligned}(\tan x)/(\sec x)&=((\sin x)/(\cos x))/((1)/(\cos x))\\\\&=(\sin x)/(\cos x) * (\cos x)/(1)\\\\&=(\sin x\cos x)/(\cos x) \\\\&=\sin x \end{aligned}`