Question

The radioactive isotope of lead, Pb-209, decays at a rate proportional to the amount present at time t and has a half-life of 3.3 hours. If 1 gram of this isotope is present initially, how long will it take for 90% of the lead to decay? (Round your answer to two decimal places.)

Answer 1

It will take 10.96 hours for 90% of the lead to decay.

Explanation:

The radioactive isotope of lead, Pb-209, decays at a rate proportional to the amount present at time t

This means that the amount can be modeled by the following function:

`A(t) = A(0)e^(-rt)`

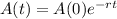
In which A(0) is the initial amount and r is the decay rate.

Has a half-life of 3.3 hours.

This means that
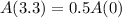`A(3.3) = 0.5A(0)`. We use this to find r.

`A(t) = A(0)e^(-rt)`

`0.5A(0) = A(0)e^(-3.3r)`

`e^(-3.3r) = 0.5`

`\ln{e^(-3.3r)} = ln(0.5)`

`-3.3r = ln(0.5)`

`r = - (ln(0.5))/(3.3)`

`r = 0.21`

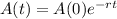
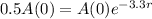
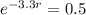
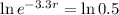
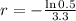
So

`A(t) = A(0)e^(-0.21t)`

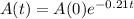
How long will it take for 90% of the lead to decay?

This is t for which
`A(t) = 0.1A(0)`, that is, 100 - 90 = 10% of the initial amount.

`A(t) = A(0)e^(-rt)`

`0.1A(0) = A(0)e^(-0.21t)`

`e^(-0.21t) = 0.1`

`\ln{e^(-0.21t)} = ln(0.1)`

`-0.21t = ln(0.1)`

`t = -(ln(0.1))/(0.21)`

`t = 10.96`

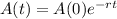
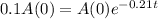
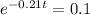
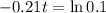
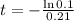
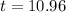
It will take 10.96 hours for 90% of the lead to decay.