Question

The Maryland State Department of Education reports that 12% of the high school students in that state attend private high schools. The University of Maryland wonders if the percentage is the same in their applicant pool. Admissions officers plan to check a random sample of the over 10,000 applications on file to estimate the percentage of students applying for admission who attend private schools. They select a random sample of 450 applications, and find that 46 of those students attend private schools.

Answer 1

The question is incomplete. Here is the complete question.

The Maryland State Department of Education reports that 12% of the high school students in that state attend private high schools. The University of Maryland wonders if the percentage is the same in their applicant pool. Admissions officers plan to check a random sample of the over 10,000 application on file to estimate the percentage of students applying for admission who attend private schools. They select a random sample of 450 applications, and find that 46 of those students attend private schools. Create and interpret a 95% confidence interval.

Answer and Step-by-step explanation: Th proportion of students that attend private schools in the sample is

`p=(46)/(450)`

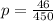
p = 0.102

At 95% confidence, z-score is 1.96.

Standard deviation for sample proportion is calculated as

`\sigma = \sqrt{(p(1-p))/(n) }`

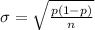
For this sample, it will be

`\sigma = \sqrt{(0.10(1-0.1))/(450) }`

`\sigma=√(0.0002)`

`\sigma=0.01414`

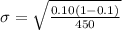
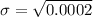
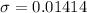
Interval is calculated as

p ± zσ

Then

0.102 ± 1.96(0.01414)

0.102 ± 0.028

Interval is 0.074 < p < 0.13

What confidence interval means is that with a certainty of 95%, we are confident that the true population proportion of students who attend private schools are between 0.074 and 0.13.