A statement that is true regarding Huy's work is: C. Huy is incorrect. He made a mistake in step 2 of the solution when he added a 9 to both sides.
In Mathematics and Euclidean Geometry, the standard form or general form of a quadratic equation is represented by the following equation;

Next, we would solve the given quadratic equation by using the completing the square method;
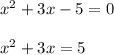
In order to complete the square, we would have to add (half the coefficient of the x-term) squared to both sides of the quadratic equation as follows:
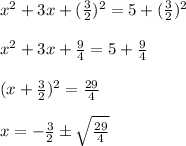
Complete Question:
Huy is solving a quadratic equation by completing the square. His first few steps (steps 1-4) are shown below. Which of the following statements is true regarding Huy's work?
Given
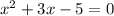
Solution
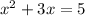 step 1
step 1
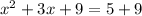 step 2
step 2
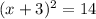 step 3
step 3
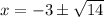 step 4(1 point)
step 4(1 point)
Huy is incorrect. He made a mistake in step 1 when he added a 5 to both sides. He should have only added a 5 to the left side of the equation.
Huy is incorrect. He made a mistake in step 4 when he solved the equation
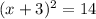 for x.
for x.
Huy is incorrect. He made a mistake in step 2 of the solution when he added a 9 to both sides.
Huy is correct. He has done a nice job of completing the square.