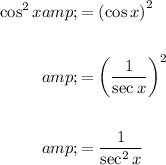Question

For each expression in the first column, choose the expression that completes an identity.

Answer 1

`\large\boxed{-\tan x \cos x} \longleftrightarrow \boxed{-\sin x}`

`\large\boxed{\vphantom{\frac12}\sec^2x - 1}\longleftrightarrow \boxed{(\sin^2x)/(\cos^2x)}`

`\large\boxed{(\sec x)/(\csc x)} \longleftrightarrow \boxed{\vphantom{\frac12}\tan x}`

`\large\boxed{1+\sin^2x} \longleftrightarrow \boxed{2-\cos^2x}`

`\large\boxed{\vphantom{\frac12}\cos^2x}\longleftrightarrow \boxed{(1)/(\sec^2x)}`

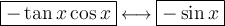
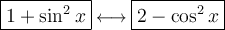
Explanation:

To rewrite -tan(x)cos(x), we can use the quotient identity:

`\boxed{\tan x=(\sin x)/(\cos x)}`

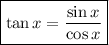
Therefore:

`\begin{aligned}-\tan x \cos x & = -(\sin x)/(\cos) \cdot \cos x\\\\& = -(\sin x\cos x)/(\cos) \\\\&=-\sin x\end{aligned}`

`\hrulefill`

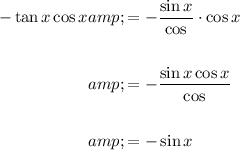
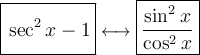
To rewrite sec²x - 1, we can use the Pythagorean identity and the quotient identity:

`\boxed{\begin{array}c1 + \tan^2x = \sec^2x&\tan x=(\sin x)/(\cos x)\end{array}}`

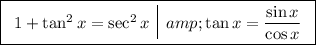
Therefore:

`\begin{aligned}\sec^2x - 1 & = 1 + \tan^2x - 1\\\\&=\tan^2x\\\\&=(\sin^2x)/(\cos^2x)\end{aligned}`

`\hrulefill`

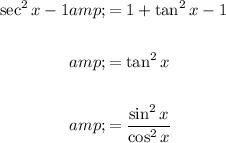
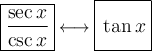
To rewrite sec(x)/csc(x), we can use the reciprocal identities:

`\boxed{\begin{array}c\sec(x) = (1)/(\cos(x))&\csc(x) = (1)/(\sin(x))\end{array}}`

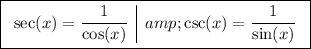
Therefore:

`\begin{aligned}(\sec x)/(\csc x)&=((1)/(\cos x))/((1)/(\sin x))\\\\&=(1)/(\cos x) \cdot (\sin x)/(1)\\\\&=(\sin x)/(\cos x)\\\\&=\tan x\end{aligned}`

`\hrulefill`

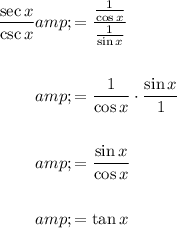
To rewrite 1 + sin²x, we can use the Pythagorean identity:

`\boxed{\sin^2x + \cos^2x = 1}`

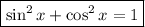
Therefore:

`\begin{aligned}1+\sin^2x&=1+(1-\cos^2x)\\\\&=1+1-\cos^2x\\\\&=2-\cos^2x\end{aligned}`

`\hrulefill`

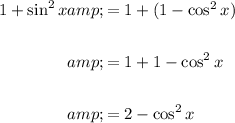
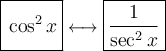
To rewrite cos²x, we can use the reciprocal identity:

`\boxed{\cos x = (1)/(\sec x)}`

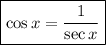
Therefore:

`\begin{aligned}\cos^2x&=\left(\cos x\right)^2\\\\&=\left((1)/(\sec x) \right)^2\\\\&=(1)/(\sec ^2x)\end{aligned}`