Question

Let R be the region bounded by the curves y = x^1/4 and y = x. Compute the volume of the solid obtained by revolving R about the axis x = 1.

Answer 1

To find the volume of the solid of revolution obtained by revolving the region R, bounded by y =
`x^{1/4` and y = x, about the axis x = 1, we use disk integration with adjusted radii and limits of integration from the points of intersection of the two curves.

To compute the volume of the solid obtained by revolving the region R bounded by the curves y =
`x^{1/4` and y = x about the axis x = 1, we can use the method of disk integration. The volume of such a solid can be calculated using the formula:

V = π ∫₁² [1 - (x - 1
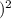`)^2`] dx, where we subtract the squared term representing the inner radius (
`x^{1/4`) from the outer radius (x), after both radii have been adjusted for the fact that we are revolving around x = 1, not the y-axis.

To find the limits of integration, we need to determine where the curves intersect, which is solved by equating
`x^{1/4` = x. This gives us x = 0 and x = 1 as our boundaries.

After setting up the integral, we compute it, and the result is the volume of the solid of revolution. This process applies calculus and geometric understanding to derive the final value.