Question

A bicycle company had designed and built a new model of sports bicycle. They had a profit for the sale of bicycles can be modeled by the function P(x)=-2x^2+920x+84,000 . where x is the price of each bicycle.

Which of the following is a sale price for the bicycles that will allow the company to profit 189,0000

Answer 1

To find the sale price that will allow the company to profit $189,000, we need to set the profit function equal to that amount and solve for x. The sale price that will allow the company to profit $189,000 is $250.

To find the sale price that will allow the company to profit $189,000, we need to set the profit function equal to 189,000 and solve for x. The profit function is given by P(x) = -
`2x^2` + 920x + 84,000. So, we have -
`2x^2` + 920x + 84,000 = 189,000. Rearranging, we get -
`2x^2` + 920x - 105,000 = 0. Using the quadratic formula, we can solve for x:

x = (-b ± √(
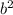`b^2` - 4ac)) / (2a)

Plugging in the values from our equation, we get:

x = (-920 ± √(
`920^2`- 4*(-2)*(-105,000))) / (2*(-2))

Simplifying, we get two possible solutions: x = 250 or x = -140. However, since we are dealing with the price of a bicycle, a negative price is not meaningful. Therefore, the sale price that will allow the company to profit $189,000 is $250.