Jeanne's loan scenario involves mathematics related to calculating loan payment details with an APR of 8.55% over 3 years. Using the principles of loan amortization and interest calculation similar to the example of Joanna's housing loan, one can determine the monthly payments and total cost of the loan.
To calculate the maximum loan Joanna can afford, we can use the present value formula. The formula is:
Loan Amount = Annual Payment / (1 + Interest Rate)^Number of Years
Plugging in the values Joanna knows (Annual Payment: $12,000, Interest Rate: 4.2%, Number of Years: 30), the formula becomes:
Loan Amount = $12,000 /
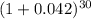
Calculating this, we find that the maximum loan Joanna can afford is approximately $202,556.98.
Another reference indicates how Charese's student loan works, with an interest rate of 6.8% over 15 years, which would require an understanding of payment calculations over the loan's term. Similarly, the situations with Tyler and Francisco involve determining the time it would take to pay off their respective credit card bills based on given APRs and monthly payment amounts.
An understanding of these concepts is crucial when Jeanne evaluates her own loan options with her bank for purchasing a car at an 8.55% APR over 3 years.