Question

Find the angle θ between
u = –8i – 3j + 5k and v = –6i + 5j + 3k.

Answer 1

The angle between the two given vectors is equal to 54.58º. (Correct choice: A)

How to determine the angle between two vectors

In this problem we must determine the measure of an angle between two given vectors, such measure can be found by means of definition of dot product:

`\vec u \,\bullet \,\vec v = \|\vec u\| \cdot \|\vec v\|\cdot \cos \theta`

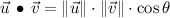
Where:

• 
  `\|\vec u\|`,
  `\|\vec v\|` - Norm of the vectors.
• 
  `\theta` - Angle between the two vectors.

And norm of a vector can be calculated by following Pythagorean equation:

`\|\vec r\| = √(x^2 + y^2 + z^2)`

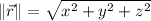
Now we proceed to make the required calculations:
`\vec u = (- 8, - 3, 5)` and
`\vec v = (- 6, 5, 3)`

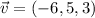
First, determine the dot product:

`\vec u \,\bullet \,\vec v = (- 8, - 3, 5)\,\bullet\,(-6, 5, 3) = (- 8)\cdot (-6) + (- 3)\cdot 5 + 5\cdot 3`

`\vec u \,\bullet \,\vec v = 48 - 15+ 15 = 48`

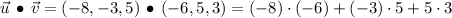
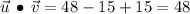
Second, determine the norm of each vector:

`\|\vec u\| = √((- 8)^2 + (- 3)^2 + 5^2)`

`\|\vec u\| = 7√(2)`

`\|\vec v\| = √((- 6)^2 + 5^2 + 3^2)`

`\|\vec v\| = √(70)`

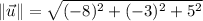
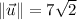
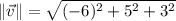
Third, determine the trigonometric function:

`\cos \theta = (48)/(7√(2)\cdot √(70))`

cos θ = 0.580

Fourth, find the angle between the two angles:

θ ≈ 54.582º