Question

Consider vectors u = 〈–3, 6〉and v = 〈2, 4〉. Write u as the sum of two orthogonal vectors, one of which is the projection of u onto v.

Answer 1

vector u can be written as the sum of two orthogonal vectors:

u = 〈9/5, 18/5〉 + 〈-24/5, 12/5〉.

To write vector u as the sum of two orthogonal vectors, one of which is the projection of u onto v, we can use the formula for vector projection.

First, let's find the projection of u onto v. The projection of u onto v is given by the formula:

`proj_v(u)` =
`(u dot v / ||v||^2)`* v

where "dot" represents the dot product and "||v||" represents the magnitude of vector v.

Using the given vectors, we can calculate the dot product of u and v:

u dot v = (-3 * 2) + (6 * 4) = -6 + 24 = 18

Next, we find the magnitude of vector v:

||v|| =
`√(2^2 + 4^2)` =
`√(4 + 16)` =
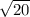`√(20)` = 2√5

Now, we can calculate the projection of u onto v:

`proj_v(u)` = (18 /
`(2√(5) )^2` * 〈2, 4〉

Simplifying further:

`proj_v(u)` = (18 / 20) * 〈2, 4〉

`proj_v(u)` = (9 / 10) * 〈2, 4〉

`proj_v(u)` = 〈(9/10) * 2, (9/10) * 4〉

`proj_v(u)` = 〈9/5, 18/5〉

Now, to find the second orthogonal vector, we subtract the projection of u onto v from vector u:

orthogonal vector = u -
`proj_v(u)`

orthogonal vector = 〈-3, 6〉 - 〈9/5, 18/5〉

orthogonal vector = 〈-3 - 9/5, 6 - 18/5〉

Simplifying further:

orthogonal vector = 〈(-15/5) - (9/5), (30/5) - (18/5)〉

orthogonal vector = 〈-24/5, 12/5〉

Therefore, vector u can be written as the sum of two orthogonal vectors:

u = 〈9/5, 18/5〉 + 〈-24/5, 12/5〉.