Hi there!
a.
To find the total amount of people that have ENTERED by t = 20, we must take the integral of the appropriate function.
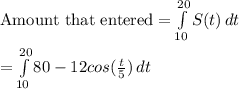
Evaluate using a calculator:
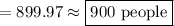
b.
To solve, we can find the total amount of people that have entered of the interval and subtract the total amount of people that have left from this value.
In other terms:
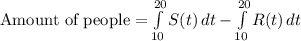
We can evaluate using a calculator (math-9 on T1-84):
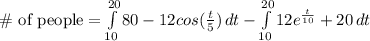
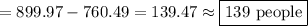
c.
If:
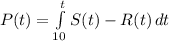
Then:
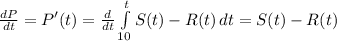
Evaluate at t = 20:

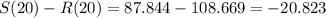
This means that at t = 20, there is a NET DECREASE of people at the movie theater of around 20.823 (21) people per hour.
d.
To find the maximum, we must use the first-derivative test.
Set S(t) - R(t) equal to 0:
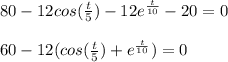
Graph the function with a graphing calculator and set the function equal to y = 0:
According to the graph, the graph of the first derivative changes from POSITIVE to NEGATIVE at t ≈ 17.78 hours, so there is a MAXIMUM at this value.
Thus, at t = 17.78 hours, the amount of people at the movie theater is a MAXIMUM.