Answer:
First equation :
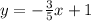
Second equation : y = 4
Explanation:
We want to write equations for the two given lines in slope intercept form
y = mx + b
Where m = slope and b = y intercept
Identifying the y intercept
First lets find the y intercept.
The y intercepts is where the line passes the y axis.
By looking at the first line it appears that the line passes the y axis at (0,1) meaning the y intercept is 1 so b = 1
Identifying the slope
We can find the slope using the slope formula
slope = (y1-y2)/(x1-x2)
Where the values of x and y derive from any two points on the line. (x1,y1) and (x2,y2)
The points used may vary as there are many options however I have chosen (0,1) and (-5,4)
So (x1,y1) = (0,1) and (x2,y2) = (-5,4)
Meaning x1 = 0 , y1 = 1 , x2 = -5 and y2 = 4
( we now plug these into the slope formula )
Again recall slope = (y1-y2)/(x1-x2)
==> plug in x1 = 0 , y1 = 1 , x2 = -5 and y2 = 4
slope = (1-4)/(0-(-5))
==> reduce subtraction
slope = -3/5
so our slope(m) is -3/5
Plugging in slope and y intercept into slope intercept form
Finally we plug in the values of m and b into slope intercept form to get the equation
Again we have y = mx + b
m = -3/5 and b = 1
So our equation is y = -3/5x + 1
Identifying equation for second line
When we have a horizontal line our equation is going to be put in y = b form where b = the y value that the line crosses. (or y intercept)
Here the line goes through the y value of 4 so b = 4
Hence, the equation of the second line would be y = 4